Mixture Experiments and their Applications in Welding Flux Design
Ademola David Adeyeye & Festus A. Oyawale
J. of the Braz. Soc. of Mech. Sci. & Eng. Copyright by ABCM
The traditional welding flux development has been by cost, material, time and labour intensive experiments. The extensive and expensive trial and error experimentation is needed because it is often difficult to know a priori how the flux ingredients interact to determine the operational characteristics of the flux and the final performance of the welded structure. The limitation of the traditional approach includes: (1) long lead-time (2) expensive experiments in terms of materials and energy consumption and labour requirements (3) the flux developed can not be guaranteed to be optimal and (4) inability to identify and quantify direct and interaction effects of flux ingredients. These constraints are due to the paucity of statistical modelling tools in welding flux technology. Since prediction models are derived from designed experiments, flux researchers need other methods by which flux experiments may be designed. This paper discusses a statistical modelling tool known as mixture experiment which has the potential to revolutionize welding flux development technology. Mixture design is discussed but not fully developed. The procedure of mixture experiment, analytical model forms and the sequence of model fitting are discussed. Areas of welding flux research where the various mixture designs may be useful are suggested.
Introduction
1 In spite of the increasing interest in the development of prediction and optimization tools in arc welding technology, the development of welding flux still remains largely on lengthy trial and error experimentation. The experiments are often based on the principles of metallurgy, physics, and chemistry tempered with experience. The extensive and expensive trial and error experiments are needed because it is often difficult to know a priori how the flux components interact to determine the operational characteristics of the flux and the final properties of the weld-metal. The traditional approach of welding flux formulation is expensive because of the long lead-time, consumption of considerable amount of costly materials, high energy consumption and labour requirement. The long lead-time is due to the lengthy trial and error experiments while the high energy requirement is due to the need for extensive experimental weld production and testing. With the traditional welding flux development approach, information on the main and interaction effects of the flux ingredients on the weld-metal properties and operational characteristics of the welding flux are not readily identified and quantified. Many investigators tried to understand the role of each flux ingredients on the weld-metal properties and operational characteristics of the process by varying only the individual flux ingredient in a given flux system (Farias et al., 2002; Du Plessis et al. 2007). Kanjilal et al., (2004) observed that this approach by its very nature failed to take into account the simultaneous variation of the flux ingredients as well as their interaction effects. The significant interactions effect of flux ingredients has been reported previously (Lau et al., 1986 and Kanjilal et al., 2004). Assessment of flux ingredient interaction has been recognised as increasingly important in welding flux design where it may be necessary to determine the combined synergetic and antagonistic effects of many flux ingredients (Kanjilal et al., 2004, 2006, 2007) Another limitation of the traditional approach is that the best among the experimental flux formulations is used as the appropriate flux for a given metal under the given welding conditions. Such welding flux has a random character and is not guaranteed to be the optimum since it is not practical to explore all combinations of compositional variation due to time and cost limitations. These drawbacks are as a result of the paucity of statistical modelling tools in welding flux formulation technology. The need for the reduction of the number of experiments has been the concern of welding flux researchers and manufacturers. Although modelling tools can not completely eliminate experiments, it can drastically reduce the number of experiments. Quintana et al (2006) observed that a reduction in the number of experimental welds from 30 to 5 in GMAW leads to about 80% energy savings. Obviously the benefits of the reduction in the number of experimental welds would be higher by the time the savings on materials, labour and time are considered. The challenge confronting the welding flux manufacturer is the need to reduce the costs of labour, energy and materials and the time to market in order to improve profitability. It is unlikely that the welding flux manufacturer will be able to rise to these challenges without better tools in the form of prediction and optimization models. To arrive at an optimum flux composition and mitigate the problems of the traditional approach, an alternative approach is to develop mathematical models through effective and strategic planning, design and execution of experiments. With the availability of such models, the formulation of welding flux can be based on quantitative footing. Such an approach minimizes the expenditure of time, labour and materials. Factorial design, which has been widely used in other areas of arc welding technology, is inadequate for welding flux formulation because flux properties depend on the relative proportions of the flux ingredients (Anderson and Whitcomb, 2002). The statistical experiment design and analytical methods developed specifically for optimizing mixtures in which the final properties depend on the relative proportions of the ingredients are the focus of this paper. Although statistical design of mixture experiment has been available for some time, it seems relatively unknown to most welding flux researchers. The efficacy of the methodology in welding flux research has been demonstrated by Kanjilal et al (2004, 2005a, 2005b, 2006 and 2007). This paper presents a brief discussion on mixture design. The procedure of mixture experiment, the analytical model forms and the sequence of model fitting are discussed but not fully developed. Areas of welding flux research where the various mixture designs may be useful are suggested.
Proposal for a New Approach
Survey of welding literature shows there is a plethora of modelling and optimization methods in arc welding technology (Table 1). However welding flux appears to be lagging behind other areas of arc welding technology due to the paucity of prediction and optimization tools. Factorial design and response surface methods appeared to be among the most widely used of the modelling tools in arc welding research. Apart from Kanjilal and co-investigators other investigators concentrated on developing models that determine the optimal setting of process factors (Table 1). Development of models should not be limited to process factors because studies have shown that flux formulation plays a prominent role in the productivity of the welding process and the quality of the welded structure (De Rissone et al, 2001; Pessoa et al, 2007; Du Plessis and Du Toit, 2007 and Du Plessis et al, 2006). Although factorial design methods provide an efficient means for the optimization of welding process, they do not work well for mixtures of which welding flux formulation is an example (Anderson and Whitcomb, 2002). A simple but effective strategy should involve:
1. Optimizing the flux formulation via mixture design
2. Optimizing the process with factorial design and response surface methods.
The latter has received much attention but little has been reported on the first. Mixture design methodologies work well for welding flux development because welding flux conforms to the key assumptions of mixture design (Table 2) but it seems relatively unknown to most welding flux researchers. Since the application of mixture design in welding flux research is scanty in the open literature we present a brief description of its methodology.
Inadequacy of Factorial Methods for Welding Flux Formulation
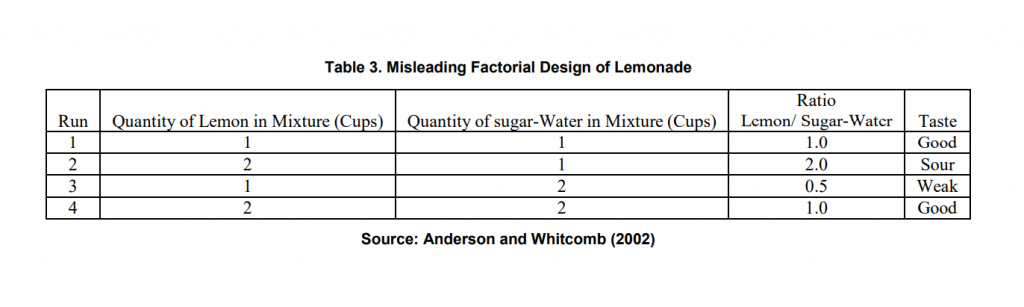
Industrial experimenters typically turn to two-level factorials as their first attempt at design of experiment (DoE). These designs consist of all combinations of each factor at its high and low levels. When the number of factors is large, only a fraction of the runs needed to be completed to produce estimates of main effects and simple interactions. However, when the response factor(s) depend on proportions of ingredients such as in food, chemical, ceramic, pharmaceutical and welding flux formulations, factorial designs may not make sense. We illustrate with the example from the paper of Anderson and Whitcomb (2002). In the lemonade experiment (Table 3), the experimenter varied the number of cups of lemon versus cups of sugar-water. Run 1 (both factors at low levels) and run 4 (both factors at high levels) taste the same. It makes more sense to look at taste as a function of the proportion of lemon to sugar-water, not the amount. As with the case of lemonade, the properties of welding flux depend on the proportions of the ingredients and not the total amount. Factorial design may not work for experiments on formulations where only proportions matter and not the amounts. Mixture design is more suitable in such cases.
Overview of Mixture Experiments
Mixture Experiments
Experiments, where the factors are the ingredients or the components of a mixture, are called mixture experiments. In mixture experiments, the choice of component levels is not independent. The response is assumed to depend only on the relative proportions of the components rather than the total amount in the mixture. Statistical experiment design and analysis methods developed specifically for the purpose of optimizing mixtures in which the final properties (responses) of the product depend on the relative proportions of the components rather than the absolute amount may be classified into two: (i) Standard Mixture Designs and (ii) Constrained Mixture Designs or Extreme Vertices Designs.
Standards Mixture Designs
In the standard mixture designs, the proportions of the ingredients can vary between 0 and 1 and must sum up to unity. Suppose we have a mixture experiment with q components, where, xi is the proportion of the ith component. Then it must satisfy the following constraints:
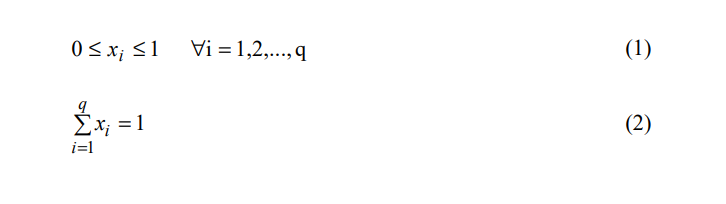
The first constraint keeps each mixture component proportion between 0% and 100% (0 and 1), and the second constraint makes sure that at any point in the mixture space, the total sum of the proportions of all the components adds up to unity. The standard mixture designs for fitting standard models are Simplex-Lattice designs (Scheffe, 1958; Gorman et al, 1962: Donzelli et al, 2003 and NIST/SEMATECH) and Simplex-Centroid designs (Scheffe 1963; Castro et al, 2003; Jang et al 2001 and Marengo et al 2006). The simplex lattice designs are also referred to as {q, m} simplex lattice designs. The q stands for the number of components, and the proportions of 0 1 2 ,…,1 m , m , are used for each component i x . The simplex-centroid designs have 2 −1 q number of distinct points. They contain every non-empty subset of the q components where the components are present in equal proportions (Scheffe 1958; Scheffe, 1963 and NIST/SEMATECH).
The standard mixture designs may not find much application in flux designs because flux ingredients rarely vary between 0 and 1. The most frequently encountered situation in flux formulation is for the flux ingredients to vary between a lower bound usually greater than 0 and an upper bound lesser than 1. The constrained mixture design or extreme vertices designs are useful for such situations.
Extreme Vertices Designs
In addition to the two constraints, there may be additional constraints imposed on the proportions of the ingredients. The constraints may be in the form of upper (Ui ) and lower (Li ) bounds,

When mixture components are subject to additional constraints, such as a maximum and/or minimum value for each component, designs other than the standard mixture designs, referred to as constrained mixture designs or Extreme-Vertices designs, are appropriate (Mclean and Anderson, 1966; Snee and Marquardt, 1974 and Ding et al, 1999). The extreme vertices design offers great potential for welding flux research. Its efficacy has been demonstrated by the pioneering work of kanji al and his co[1]investigators (Kanjilal et al, 2004, 2005, 2006, and 2007).
Mixture Amount Designs
Mixture experiment methodology has been extended to cater for situations where the response factors depend on the proportions of ingredient and the amount of the mixture. A common example of the application on mixture-amount designs is the formulation of fertilizers composed of different proportions of nitrogen, phosphate and potassium. The experimenter wishes to investigate how much fertilizer to apply, as well as to find the best relative proportions of the main components. For this kind of mixture-amount experiments, several levels of total amount are needed. The amount can vary between some minimum and maximum value so that:
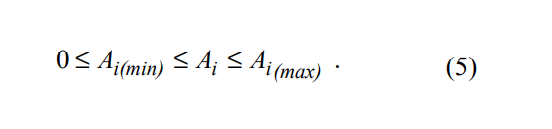
Several models have been proposed for fitting data from mixture amount experiments (Presscott and Drapper, 2004). As far as we know, application of mixture-amount designs to welding flux development has not appeared in the published literature. This design may be found useful in flux development situations in which the formulator is interested in the proportions of flux ingredients and the coating factor of coated electrode or the flux height in the case of submerged arc welding.
Mixture Process Variable Designs
Another extension of mixture experiment which may be very useful in welding flux research is the mixture-process variable designs. In many industrial processes with mixtures, the end-product quality depends both on the proportions of the mixture components and on the levels of the process variables. This type of situations is often encountered in welding processes, where the quality of the welded structure depends on the proportions of the flux components and on the levels of the process variables such as voltage, current, welding speed, etc. The process variables can be controlled independently of one another and of the mixture components. For example, in welding production system, the composition of the flux involves mixture variables while the settings of the voltage, current, welding speed, and nozzle-to-plate distance are process variables. As far as we know, Kanjilal et al, (2006) is the only work that has appeared in the literature where mixture-process variable design was applied in flux research. Analytical models develop from mixture-process variables data will quantify the synergetic and antagonistic effects of flux[1]process variable and process-process interactions. Additional information on mixture-process variables experiments can be found in the work by Scheffe (1963), Piepel and Cornell (1987), Goldfarb et al (2003, 2004) and Mage and Naes (2005).
Typical Procedure of Mixture Experiment
The steps a welding flux researcher may follow in planning mixture experiments typically involve the following procedures (NIST/SEMATECH, Gunaraj and Murugan, 2002 and Allen et al,2002):
• Define the objectives of the experiment
• Select the flux ingredients and where necessary any other
factor to be studied e.g. process variables
• Identify any constraints on the flux components or other
factors in order to specify the experimental region.
• Identify the response variables to be measured
• Propose an appropriate model for modelling the response
data as functions of the flux ingredients and other factors
selected for the experiment
• Select an experimental design that is sufficient not only to fit
the proposed model but which allows a test of model
adequacy as well
• Conduct the experiment as per the design matrix
• Measure and record the responses
• Develop the mathematical models
• Calculate the coefficients of the polynomials
• Check the adequacy of the model developed
• Conduct the confirmatory test
• Present the main and interaction effects of the different
ingredients on the responses
• Use the model to predict the combination of flux ingredients
that will give the desired response
• Perform actual experiments with the designed flux
• Analyze the results
The Analytical Model Forms
Due to the ∑xi = 1 constraint, the form of the mixture model is different from the general polynomials used in the response surface methodology. The general response surface polynomials are reparameterized to take care of this constraint. Some of the most commonly used model forms appropriate for fitting mixture data are listed below. The mixture experiment literature is extensive; therefore the list presented below is only illustrative and not exhaustive. More information about these model forms can be found in the reference given with each model.

Draper and St John (1977) extended Scheffe’s models with term of the form xi power to -1 added to reflect the possible extreme changes in the response that sometimes occur in some mixture problems as the value of certain components tend to a boundary value ( xi →∈i ). These terms or their coefficients were referred to as the edge effects. These models should be used for predictive purposes without attempting to place specific meaning on individual coefficient. If the experimenter suspects that only one or two components may be subjected to edge effects, he could include only terms in xi power to -1 for those components.



Model Fitting
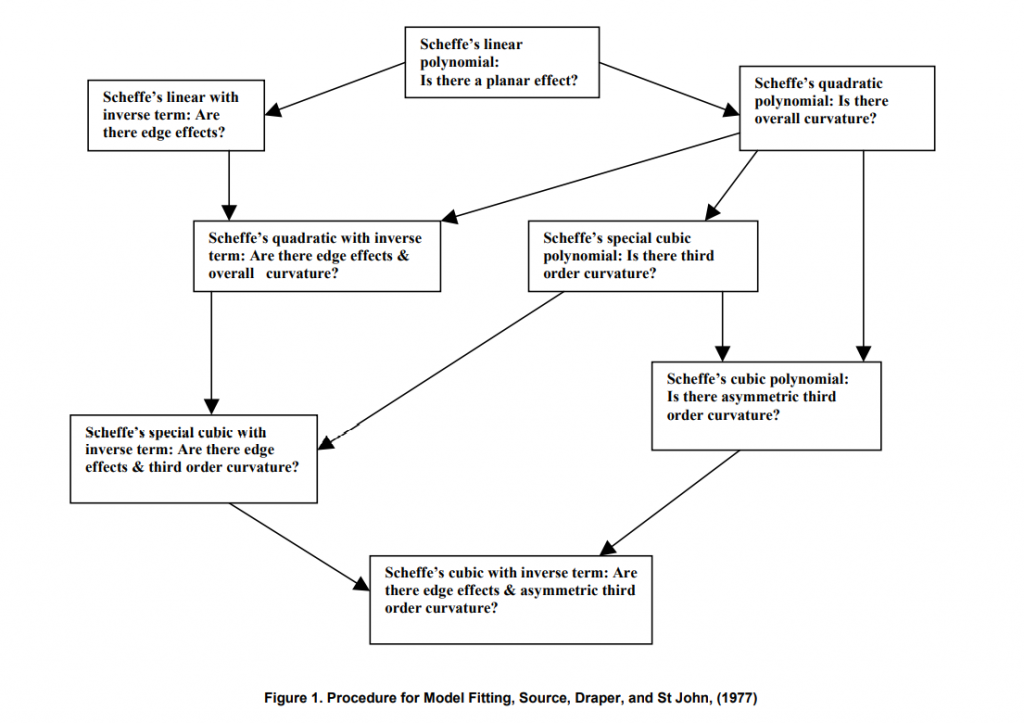
We illustrate the model fitting procedure with the case where the flux formulator is interested in the response curvature and possible edge effect. The formulator may first fit the Scheffe’s linear canonical polynomial and make a judgment about the adequacy of this model to fit his data. If he deemed the model inadequate, he could fit the Scheffe’s second order polynomial to see if there is an overall curvature or scheffe’s linear with inverse term to see if there is edge effect. Figure 1 shows the alternative sequential model build-ups that are available. The flux formulator can sequentially build up a model to any desired complexity by starting with the Scheffe’s linear model and proceeding on indicated paths through figure 1 until an acceptable model is obtained.
Conclusion
A statistical modelling tool known as mixture experiment, which has the potential to revolutionize welding flux development technology was discussed. The major conclusions are presented as follows:
- Mixture experiment can be used in welding flux development because flux properties depend on the proportions of ingredients.
- Standard mixture designs such as simplex-lattice and simplex-centroid will have limited applications in welding flux research because flux ingredients usually vary between a lower bound greater than 0 and an upper bound lesser than 1 (100%).
- Extreme Vertices Designs are most appropriate when the researcher is interested in the effect of flux ingredients proportions on the responses.
- Mixture-amount Designs are suitable for situations in which the researcher is interested in the effect of ingredient proportions and other factors such as coating factor for coated electrodes or flux height in the case of submerged arc welding.
- Mixture-process Variable Designs are suitable for cases where responses of interest depend on the proportions of ingredients and the levels of process variables.
Know-More